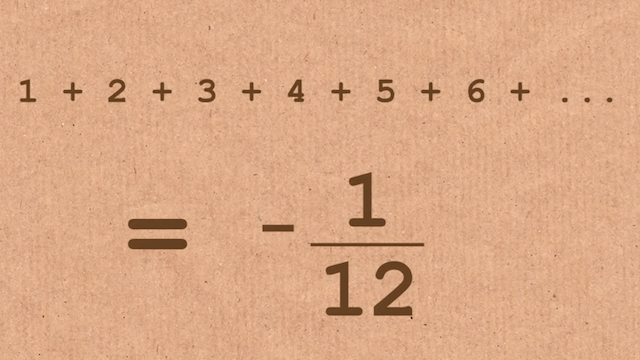Here’s a fun little brain wrinkle pinch for all you non-maths people out there (that should be everyone in the world*): the sum of all natural numbers, from one to infinity, is not a ridiculously big number like you would expect but actually just -1/12. Yes, the sum of every number from one to infinity is some weird negative fraction. What the heck?
I’m not a maths guy but I’m pretty good at basic arithmetic. By that I mean I’m pretty good at adding really small numbers. By that I mean I would totally figure that if you add all the numbers until infinity, you’re going to get a really big number. Not in this case. It seems like some mathematic hocus pocus at work here but it’s real.
What’s fascinating is that this idea that the sum of all natural numbers is -1/12 actually popped up way back in 1735 (as pointed out by Kottke). But seeing all those numbers actually come out to -1/12 is a whole ‘nother story. So watch physicists Tony Padilla and Ed Copeland from the University of Nottingham walk through the process of getting -1/12. The video by Numberphile is fascinating because it’s mind-blowing but also because you can see the real joy from the wonderful people proving this. I love it. I love them. I like maths a little more.
*Genius humans, please forgive us normal civilians for not taking advanced maths classes and forgetting how to calculiing the calculus. We know maths people exist somewhere.