Black holes may be one of the universe’s most bizarre phenomena. They’re literally divide-by-zeros in the sky, places where the mathematics of Albert Einstein’s theory of general relativity falls apart. These dense behemoths have such strong gravitational fields that time stops, and all futures point directly at the centre, and light crossing the boundary, or event horizon, can’t escape. But no one’s ever taken a picture of a black hole, and scientists want to change that.
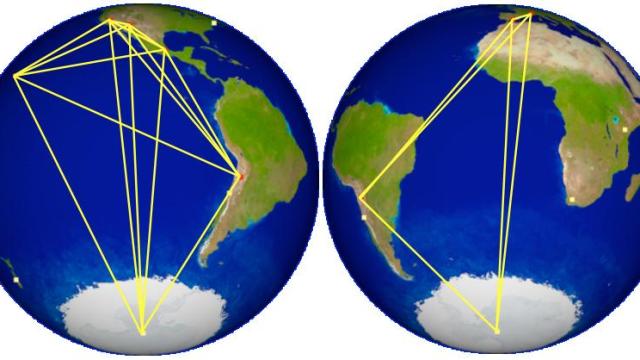
The Event Horizon Telescope, or EHT, is a network of around 10 radio telescope observatories across the planet, synchronised via the most precise atomic clocks, and pointed directly at the centre of our galaxy. There, scientists are pretty sure a supermassive black hole around four million times the mass of our Sun, called Sagittarius A*, powers the orbit of the Milky Way’s rotation, tears matter to shreds, and flings balls of it across space. The telescope network will also look at the much larger black hole inside the giant galaxy M87. The EHT is around a decade old, but the addition of the world’s most powerful radio telescope, ALMA or the Atacama Large Millimetre Array in the Chilean desert, along with a telescope at the South Pole, may allow scientists to finally get the wild black hole image previously offered only by artist drawings or computer simulations.
This souped-up Event Horizon Telescope will start observing in early April.
“This is going to be a seminal observation in the history of mankind,” Grant Tremblay, observational astrophysicist from Yale University, told Gizmodo. “This image [of Sagittarius A*], whatever it shows, will be in the top ten images ever taken.”
The EHT made its first failed black hole observations in 2006. But then, scientists confirmed it could resolve black hole-sized structures with data from the 2007 observing run, Shep Doeleman, the astronomer directing the effort, explained to Gizmodo. The method used to link all of its telescopes into one, called Very Long Baseline Interferometry, isn’t new either — scientists published a paper on the “first global radio telescope” back in the mid 1970s when people started connecting radio telescopes across ten to hundreds of kilometres. Despite that, we don’t have a crisp image of a black hole or the shadows they cast, because the telescopes’ combined resolutions haven’t been high enough. We just have a lot of tantalising hints — we’re fairly certain Sagittarius A* is a black hole, and we know that it has a disk of matter orbiting it.
ALMA and the South Pole Telescope haven’t been hooked up to the network until this upcoming 2017 observing run, which will now include nine scopes after a few swaps. The new telescopes will allow us to capture an image of the black hole at the centre of M87 and Sagittarius A* with higher resolution than any image prior, test Einstein’s theory of relativity which says that black holes should look like a dark shadows, and understand how and why the matter orbiting black holes behaves the way it does.
EHT sites (Image: The University of Arizona)
Regular telescopes can’t see a supermassive black hole — not because it’s too dark, but because it’s way too light. The gravity of black holes causes orbiting matter to travel at rip-roaring speeds, approaching the speed of light. The immense friction between particles in the hot gas generates a bright glow, which prevents us from seeing the shadow of the light-eating Unicron itself. The interstellar matter between us and the black holes, as well as the Earth’s own atmosphere, can also blur or dim incoming light waves, depending on their properties, said Doeleman. That means there’s a Goldilocks frequency of light that black hole hunters allow into their telescopes. Rather than using visible, ultraviolet or infrared light, the EHT filters out everything except radio waves, longer light rays whose wave peaks have around a millimetre of space between them. For comparison, visible lights waves have about a thousandth to a ten thousandth that distance between their peaks.
But individual radio telescopes can only get a limited amount of information. That’s where VLBI comes in. This technique combines information from the pairs of telescopes, called baselines, clocking the infinitesimal difference in the amount of time it took the light to arrive at either, and correlating the radio wave signals with the time as measured by the atomic clocks. All those baselines essentially create one enormous telescope with a giant light-collection area — but rather than light waves meeting in one place as they do in a regular telescope, their data meets at a supercomputer later. Software lines up the shapes of the light waves as if they were all collected at the same time, a bit like how DJs use sound editing software to sync up music through a process called interferometry — the garbage cancels out, and the important stuff adds up, boosting its signal. That allows scientists to get hyper-fine resolutions. The updated EHT will be able to resolve a volume of space around Sagittarius A* with a radius equal to the distance between Mercury and the Sun, Tremblay said. That’s pretty good for something more than 25,000 light years away.
Despite years of VLBI efforts, the Chilean radio observatory called ALMA couldn’t simply plug into the network as soon as it went online — these telescopes need all the appropriate data analysis hardware and software, including quarter-petabyte disks, and a precise atomic clock, Dan Marrone, experimental astrophysicist in the Department of Astronomy at the University of Arizona, told Gizmodo. ALMA, whose inauguration was only four years ago, couldn’t rush into action, despite badgering from the EHT community. “There was a lot of pressure on ALMA to get set up in time. The rest of the Event Horizon Telescopes were relying on the Chilean array’s sixty-plus dishes to get up and running,” Violette Impellizzeri, Operations Astronomer at ALMA, told Gizmodo. “The timing was not ideal,” of getting ALMA online and trying to plug it into the EHT simultaneously.
And the EHT is just one of ALMA’s many goals. “If you wanted to look at a galaxy you need a large angular telescope” like ALMA, said Impellizzeri. Compared with the larger and further objects ALMA is capable of imaging, the EHT is like a microscope, working best for relatively small, specific sources of light.
Sometimes, the collaborative EHT science didn’t feel like a priority at ALMA. “I was very scared it wasn’t going to happen. Sometimes I wouldn’t get answered and had to wait,” said Impellizzeri. She had to be ALMA’s EHT’s advocate. “I would jump up and down. We’d go for beers with the management and I’d say, ‘Guys, this is super cool! We have to do this!’” Folks eventually got the picture. “It’s very different now, it’s the highest priority.”
ALMA is now one of the most important telescopes to the EHT’s upcoming two-week observing period. Should snow or rain fall in the Chilean desert during those two weeks, none of the EHT telescopes will run, said Impellizzeri. ALMA is a no/no-go facility.

Image: ALMA (ESO/NAOJ/NRAO)
There are other crucial telescopes lending their disks to the mission in April, like the South Pole Telescope. “We can always see the galactic centre from the South Pole,” said Marrone. Plus, pictures imaged from North-South pairs tend to be the crispest, he said. Scientists theorise this effect comes from magnetic fields between us and the black holes.
Ultimately, all of the telescopes are important. Should one telescope fail to make observations due to bad weather, that’s less information to build the image. “If you start losing one of your dishes, you’re essentially ripping off a piece of the Earth-sized telescope,” said Doeleman.
During the upcoming EHT run, scientists will mainly monitor the telescopes and perform maintenance. The run will start by collecting 3mm light waves during its first few days, and then it will move on to one or so millimetre waves for the remaining period, gathering different kinds of light for different kinds of images. After that, researchers ship all the disks — petabytes worth of data — to a central supercomputer at the Haystack Radio Observatory in Massachusetts and another in Bonn, Germany. There, the light signals’ times can be correlated and researchers can run mathematical models based on the data to actually produce the image. That requires intense pattern-matching and data machine learning algorithms — there are an infinite number of pictures that could potentially fit the data. The algorithms, written in part by MIT graduate student Katie Bouman, try to pick the image that best matches what makes the most sense from a physical perspective.
That means we won’t see the EHT’s black hole picture until much later this year at the earliest, maybe not until next year. All of those telescopes might even need to clear their schedules for another observing run next year before we see anything meaningful. “I’m not 100 per cent sure that this year they will get the result they expect,” said Impellizzeri, meaning a full-blown black hole picture. “Within the next couple of cycles they will. But this is the first result.”
No one really knows what we’ll be seeing yet, but people have some ideas. “If you had a hell of a pair of sunglasses and SPF a trillion sunscreen and a magical spacecraft,” said Tremblay, then black holes might look similar to (but not the same as) the black hole from the movie Interstellar — a black disc with light rays bent by gravity creating a solar eclipse-like glow behind it, marked with a cloud of bright, orbiting matter. Doeleman’s simulations show a crescent moon of light with the black hole’s shadow in the foreground. Maybe the black hole will have bright jets of light emanating from the top and bottom. “Regardless of what we find,” said Tremblay, “the answer will be equally astounding.”
Plus, said Doeleman, we might be able to collect information on how quickly matter orbits Sagittarius A*, and the black hole inside M87, which, despite being much further away from us, is also much larger.
After that, we can only get bigger and better. For instance, Doeleman plans on adding a telescope in Greenland to better image M87. We can even begin taking more detailed measurements on other sources in the sky. “Certainly other quasars,” bright distant light sources, “will be of interest, different active galactic nuclei jets,” beams of matter flying out of galaxies’ bright centres, “and accretion disks,” disks of matter orbiting sources of gravity, said Lynn Matthews, Research Scientist at the MIT Haystack Observatory. “We also expect to look at other types of sources, pulsars, dying stars… I think those are some of the main targets in the coming years.” And why not create a telescope even bigger than our planet? “I think people are already talking about a space based satellite,” said Avery Broderick, Associate Faculty at the University of Waterloo and researcher at the Perimeter Institute. “It would be wonderful because it is in fact [effectively] making the Earth bigger. You’ll also add zeros the price tag.”
Now, scientists are just crossing their fingers hoping the April run goes well. “It’s super exiting,” said Impellizzeri. “Even being live with other telescopes, [this run] is super exciting. I’m a bit scared. I’m not worried, but I’m nervous.”