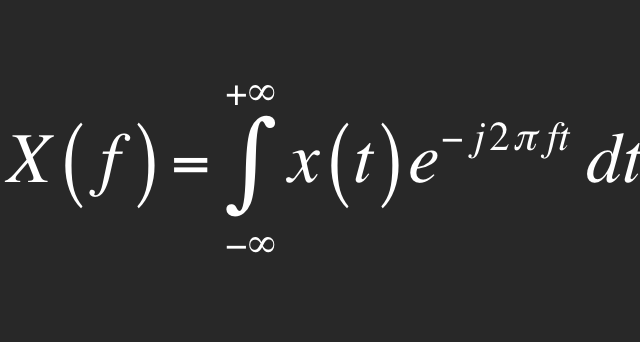This is the Fourier Transform. You can thank it for providing the music you stream every day, squeezing down the images you see on the internet into tiny little JPG files, and even powering your noise-cancelling headphones. Here’s how it works.
The equation owes its power to the way that it lets mathematicians quickly understand the frequency content of any kind of signal. It’s quite a feat. But don’t just take my word for it — in 1867, the physicist Lord Kelvin expressed his undying love for this fine piece of mathematics too. He wrote, “Fourier’s theorem is not only one of the most beautiful results of modern analysis, but it may be said to furnish an indispensable instrument in the treatment of nearly every recondite question in modern physics.” And so it remains.
Maths Will Tear Us Apart
The Fourier transform was — perhaps unsurprisingly — developed by the mathematician Baron Jean-Baptiste-Joseph Fourier and published in his 1822 book, The Analytical Theory of Heat. The Baron was interested in the way heat flowed inside and around materials, and in the process of studying this phenomenon he derived his transform. At the time, he wouldn’t have realised just how important a contribution he was making — not just to maths and physics, but science, engineering and technology as a whole.
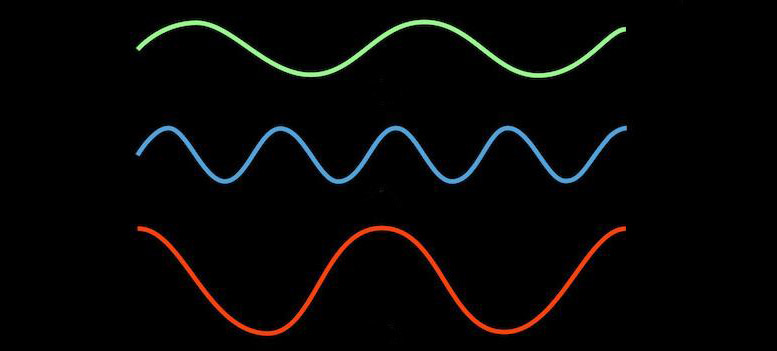
His major breakthrough was realising that complicated signals could be represented by simply adding up a series of far simpler ones. He chose to do it by adding together sinusoids — those oscillating waves you learned about in high school that wander between peak and trough with predictable regularity. Say you strike a chord on a piano, pressing three keys. You produce three different notes, all with well defined frequencies — referred to as pitches when we’re talking about audio — that look like nice, friendly sine waves:
But add them together, and that pleasant sounding chord actually looks altogether more messy, like this:
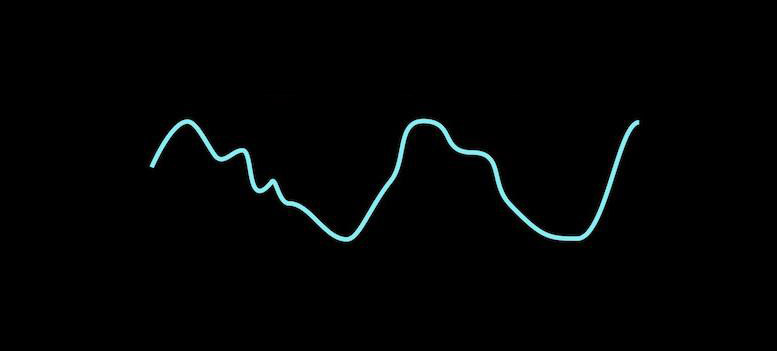
It looks complicated, but we know that fundamentally it’s just three plain sine waves staggered in time and added together. Fourier’s brain wave was to realise that however complicated the final waveform is, it can always be represented as a combination of sinusoids — even if it means using an infinite number. The real genius of this realisation for me is that if you can work out which sinusoids need to be added together to create the final waveform, you known exactly which frequencies of waves need to be added together — and in which quantities — to represent the signal. With that knowledge, you know the exact frequency content of your final signal.
That’s what the equation at the top of the page does in one fell swoop. The x(t) term represents the big, complicated signal you’re trying to represent by simpler ones. The e — jπ2ft term looks a little terrifying, but it’s actually just shorthand that mathematicians use to represent those sinusoids we’ve been talking about. The neat bit is that multiplying the two together and then wrapping them in an integral — that curly line at the front and dt term at the end — allows the equation to pick out each and every frequency component of sinuoids that are required to represent the signal. So the result of the equation, X(f), provides the magnitude and time delay of each of the simple signals you need to add together.
That is the Fourier transform: a function that explains exactly what frequencies lie in the original signal. That may sound trivial. It isn’t
Transmission
Imagine you’re in the business of sending audio files over the Internet. You could just send the whole song down the pipe in the way the music label initially records them — but they’re rather large that way. The reason for their size is that they’re a full, loss-less recording: each and every frequency is preserved from recording, through mixing, to the final track. Take a Fourier Transform of a tiny snippet of a track, though, and you’ll find that there are some frequency components that are incredibly dominant and others that barely register.
The MP3 file format does exactly this — but it tosses to one side the barely perceptible frequency components to save space, as well as some of the ones at the upper end of our hearing range because we find it difficult to distinguish between them anyway. It does that all the way through the song, chopping it into millions of sections, determining the important frequency components, junking those that are unimportant, until it’s done. What’s left are just the most important frequencies — or notes — that can be played into your ears to (pretty accurately) represent the original track. Oh, and a file that’s less than a tenth of the size, too.
It’s also very similar to how Ogg Vorbis, the file type used by Spotify for the desktop client, works (actually, Vorbis uses a fast-as-lightning computational version of the Fourier transform called a discrete cosine transform, but it’s broadly speaking the same idea.) Incidentally, Shazam uses these same transforms too — it has a database of distinctive frequency content in songs that it pairs with what you play to it, because that’s more reliable than matching the actual audio recording to another. And while we’re talking about audio, your noise-cancelling headphones use Fourier transforms, too: a microphone records the ambient noise around you, measures the frequency content across the entire spectrum, and then flips the content to add sound into your audio mix that will cancel out the crying babies and road noise that surround you.
But Fourier’s equation is not a one trick pony. So far I’ve only talked about time signals like audio — but he developed it in the first instance to help him solve problems relating to the flow of heat through materials. That means it also works in problems that are spatial. For Forueir that meant adding together simple types of 2D heat flows to represent far more complex ones. But in much the same way the Fourier transform can be used to build up digital images more efficiently than doing it pixel-by-pixel.
Loss-less image files have the colour of each and every pixel defined separately. When you save one as a JPG, the entire image is split up into smaller chunks and the 2D Fourier transform of the block taken. That provides a description of the spatial frequencies of how colour and brightness changes over this small patch of the image. Just like in the case of MP3, a JPG tosses aside some of the high-frequency components, which in the case of an image provide the sharp, crisp detail. For most of us, our eyes can’t really spot subtle differences in colour anyway, so binning the frequency components that provide pixel-to-pixel variation barely even shows anyway. Obviously if you crank the compression up you start throwing lower and lower frequencies out, too — and that’s when things can start to look a little blocky, as the colour variations between the sub-blocks become more apparent.
For all but the best-trained eyes and ears, compression systems like MP3 and JPG are barely perceptible most of the time — they look and sound great, but manage to take up a fraction of the space that their loss-less siblings demand. In other words, they make digital images and music practical, allowing us to share them easily — an utterly amazing feat for a single equation. No doubt Fourier, practical enough to write a book about heat flow, would approve.
This is the first in a new experimental series called Favoured Equation. Each month, we’ll dive into a piece of maths that makes your life easier in some way without you even realising it.
Pictures: Christine Daniloff/MIT