I’ve been fascinated with this premise for years now, and this week I saw the popular graphic below pop up yet again. I’d seen this graphic debunked, but it wasn’t particularly rigorous, so I decided it was finally time to sit down and answer this for myself definitively.

In researching this, the first thing to go looking for seemed to be whether or not the designer of the logo, Rob Janoff, has spoken about his process. Indeed, Janoffhas addressed in an interview the evolution of the shape:
The apple shape changed slightly from my original design in the early 80’s. The design firm Landor & Associates made the changes. They brightened the colours, they made the shapes much more symmetrical, much more geometric. When I designed it I pretty much did it freehand.
Pulling up examples from old Apple paraphernalia confirms that his logo was obviously not reliant on strict geometry:

OK, the original logo was not the mathematical masterpiece (mathterpiece?) that we know today, but maybe Landor & Associates introduced the golden ratio when they touched it up. I couldn’t find any information online about their design process, but in looking at examples of the Apple logo after L&A worked on it in the early ’80s, you can see it was much closer to the logo we know today:

This is from the sales manual for the original Macintosh. Here the shape is more square and symmetrical, the lines are not freehand, defined by simpler, stricter curves.
But does it adhere to the golden ratio? Absent firsthand information from the designers, our best bet is to just examine the logo ourselves. Every Apple computer contains a vector cut of the logo, in the form of a Unicode symbol — .
Additionally, Apple provides press materials directly on their site, including assets that contain a vector version of the logo. Some of the files contained in the press kit are for retina displays, so I think it’s safe to assume that the logo asset used is contemporary enough for our discussion.
Curiously, the Unicode symbol and the press kit symbol actually adhere to different geometries:

This level of variability suggests that the logo’s geometry isn’t exceptionally rigid, which sucks some of the magic out of the notion that Apple has ruthlessly machined this perfect shape. But let’s set that aside and use the most recent cut of the logo, assuming that one is the most refined.
The simplest place to start anchoring our measures is the circle marked “13” in the diagram, as the diameter runs from one point in the shape to another which makes it simple to create a circle of that precise size.

The next step is to start matching circles to curves, and seeing if their relative diameters match with the diagram.
As it turns out, most of the large curves in the Apple logo are not actually circular arcs. Taking the leaf as an example, you can see the arc intersects with the circle at both beginning and end but otherwise does not consistently follow the same curve:

This arc of the leaf is actually two separate arcs with different radii, you can see a midpoint there. This is actually the case with most of the curves in the logo. If the curves are not circular arcs, then one can’t actually use circles to generate this logo, nor can one accurately evaluate their equivalency.
But let’s forgive that, and approximate as best we can, accepting more variation. I started with the 8’s, sizing circles until they ran approximately parallel with the logo. Here were my results:
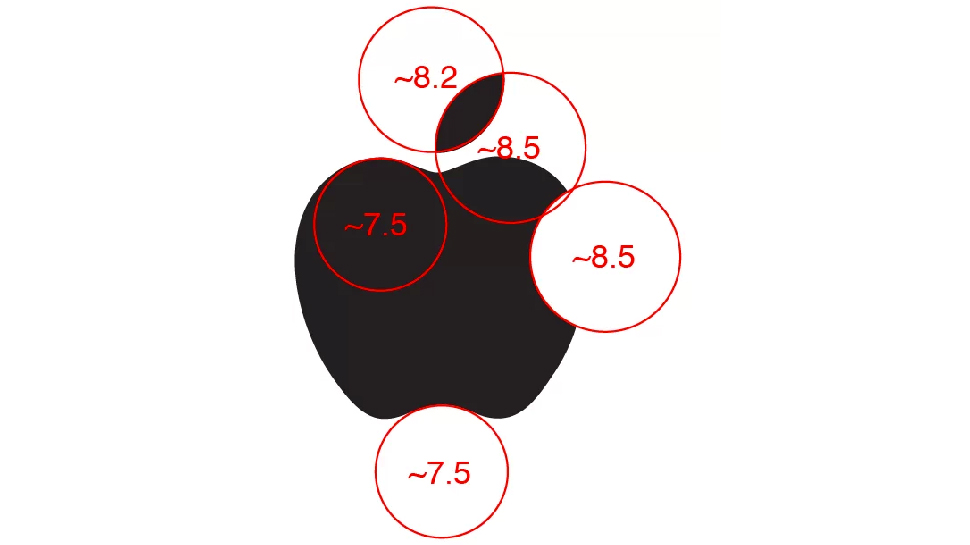
Already we have major problems. The difference between 7.5 and 8.5 is the difference been having a golden ratio value of 1.53 and 1.73. To visualise what a significant difference that is, here’s a “golden” rectangle formed out of 1.73:
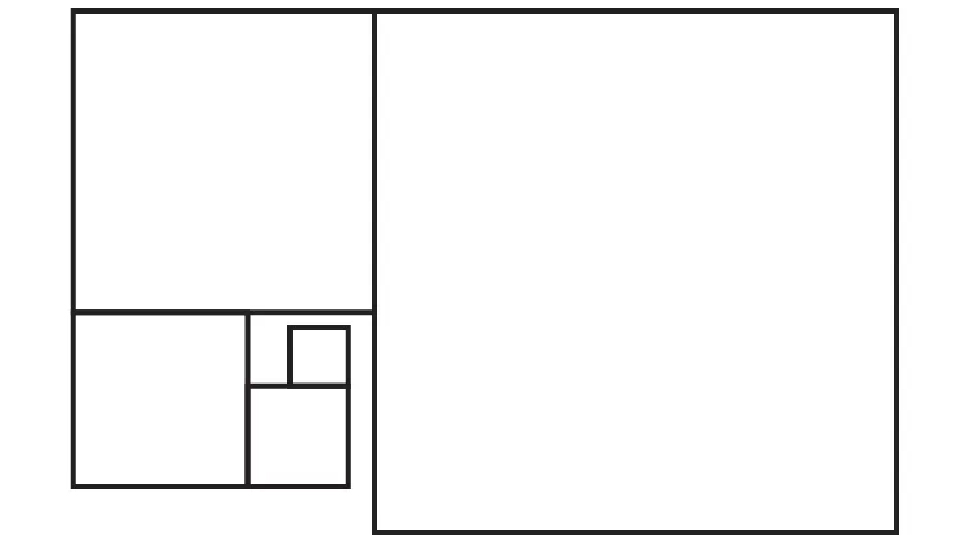
And another formed from 1.53:
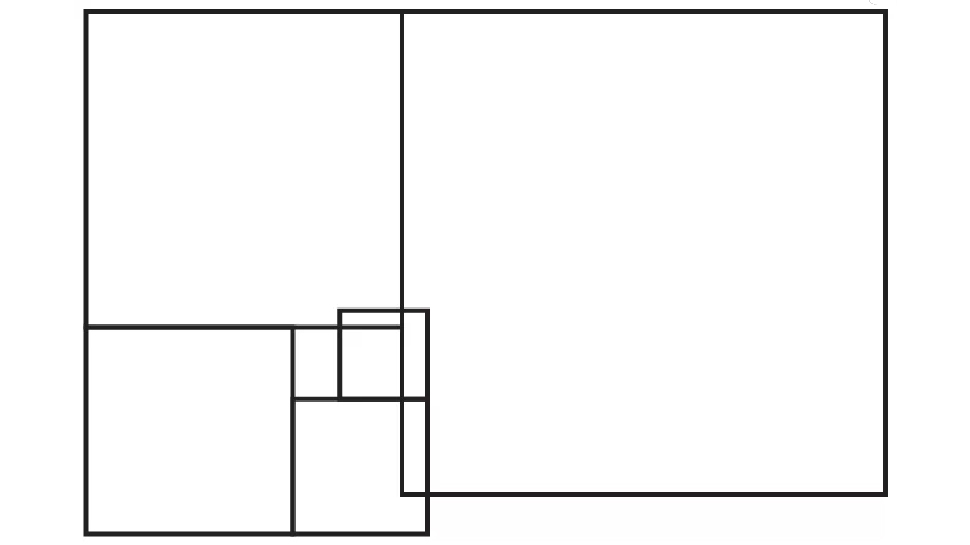
This is a dramatic amount of variability if we really are meant to place faith in an irrational number. But let’s forgive this too and look at the very rough divisions of space presented by the graphic. That bottom left corner where the 8 and the 5 meet the 3 — the only 3 mind you — is deeply suspect. Let’s take a closer look. Start by adding the 5…

Err, I mean, the 4.4…

And now the 3…
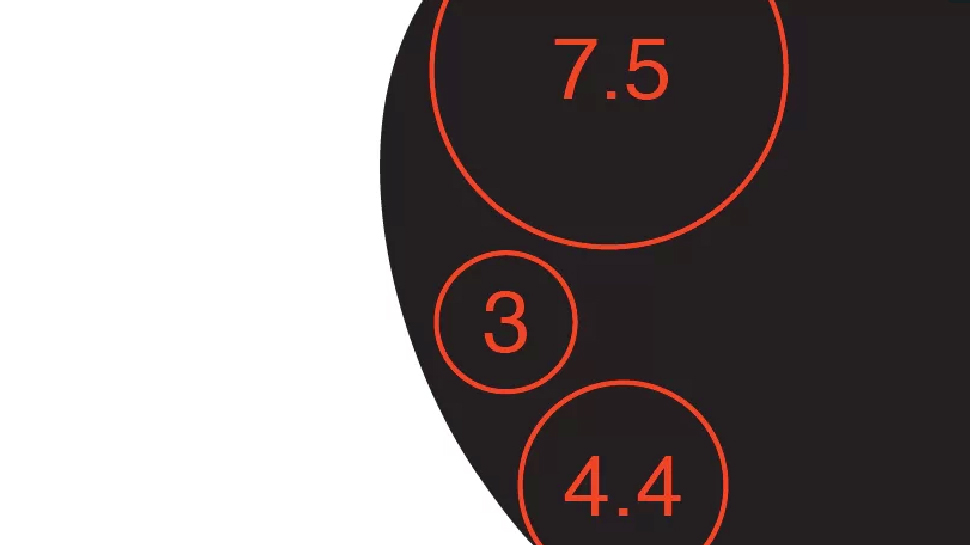
So, once you factor in the real, non-circular curves of the design, the variability really starts to demonstrate that the relationships are completely meaningless. Irrational numbers are not fuzzy things that can be loosely approximated at this magnitude. 3:4.4:7.5 is no longer maths.
But heck, let’s even forgive this and restore their circles to the fuzzy approximations:
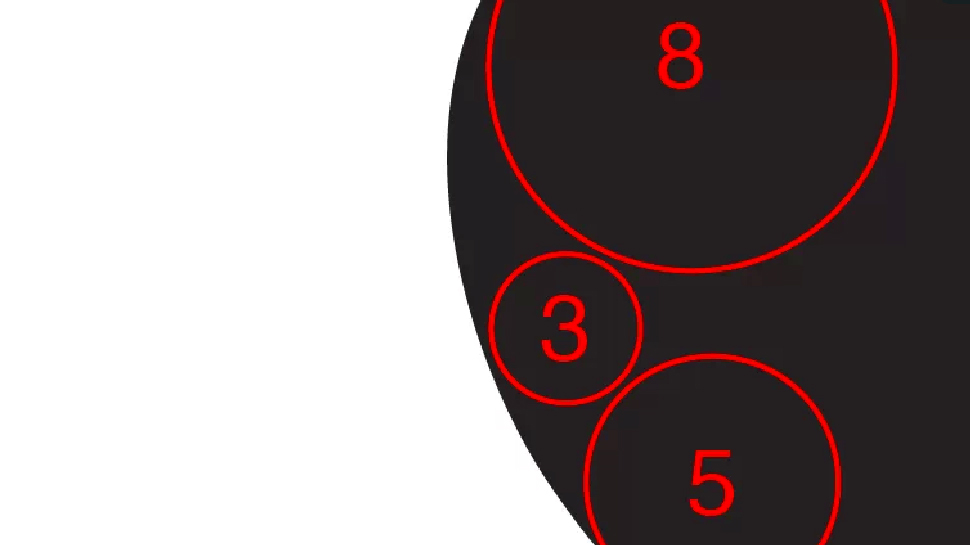
These don’t even touch when I accept the original values, but whatever.
Here’s my point: why 3? Why not this?

The condition for a space haviIt’s not as though the “1” size in the diagram is derived from some fundamental base unit: it’s just a random gap between arbitrarily defined circles.
So when you forgive the golden ratio not being used in the design process, and you forgive the fact that the logo cannot actually be derived from circles, and you forgive the fact that even approximated circles don’t line up with the proposed values, and you forgive the fact that any shape can be filled with circles of arbitrarily small diameters… what are you left with?
Let’s take a moment to consider the capital T in Helvetica:initely decreasing size. Behold, the leaf itself is a derivation from the golden ratio:

This letter is constructed to look as though the horizontal and vertical strokes have the same width. Here’s how they really compare:

They’re actually rather different. But the letter works, because the eye does not actually perceive precise geometry to be precise geometry. If they were the same width, the horizontal stroke would actually appear to be thicker and it would look bizarre. That’s the converse: real visual rhythm is hurt by precision. This fact is where we get the saying in design: if it looks right, it isright.
So in a funny way, the Apple logo feels like it adheres to some system because it doesn’t.
I’ll close with this, a mockup I made the last time I got real huffy about the golden ratio’s utility in making decisions:
This post was originally published on Quora.
