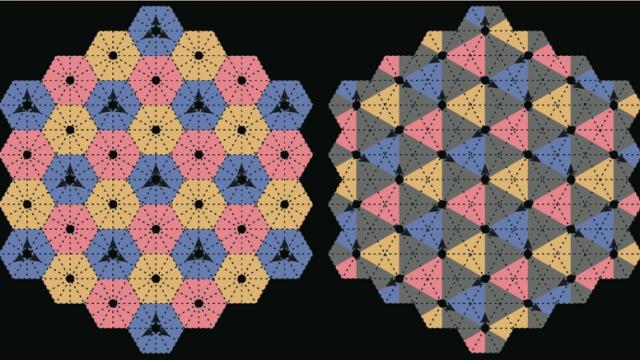
The very definition of a crystal relies on the notion of symmetry: the atoms line up in highly ordered, repeating honeycomb patterns, and that symmetry should be evident whichever way you look at it. Now physicists have stumbled upon a new type of crystal inspired by the orbits of satellites.
As described in a new paper in Physical Review Letters, rather than exhibiting symmetry in the structure — the way its atoms are arranged — this new type of crystal’s symmetry lies in how its particles move. In fact, you probably wouldn’t notice the symmetry at all in a still image of the crystal. Only if you made a movie that captured all that atomic motion over time would the hidden “choreography” finally reveal itself. It’s a type of “translational symmetry.” If you can divide a structure into a sequence of identical figures, like a wallpaper border patterned with a straight line of stamped identical cars, you have a translational symmetry.
Latham Boyle, a theoretical physicist at the Perimeter Institute of Theoretical Physics in Waterloo, Ontario, stumbled upon this strange class of objects while pondering a very different problem: how to enhance the capabilities of a future space-based gravitational wave detector — a possible heir to the recently launched LISA Pathfinder. LISA is comprised of three satellites trailing the Earth as it orbits the sun, bouncing laser beams back and forth to each other in a triangular formation. A passing gravitational wave would disrupt that constant communication, and the disruption would be picked up by highly sensitive detectors.
LISA is a beautifully designed experiment — Boyle is quick to sing its praises — but it never hurts to brainstorm ideas for future missions. Having four satellites instead of three would enable physicists to more precisely determine a gravitational wave’s amplitude (its volume or height, if we’re likening it to a sound or ocean wave), polarization (the plane along which it vibrates), and from which direction it is travelling. But it’s a much more complicated (and expensive) engineering challenge to build such an instrument. And as Boyle soon discovered, finding a symmetrical four-satellite orbit proved impossible.
Eventually he had a breakthrough: he was trying to apply a static (fixed) form of symmetry to dynamic (moving) objects. What if he could find a corresponding dynamic symmetry? To Boyle’s surprise, it worked. He found that a four-satellite system has a very high dynamic symmetry — in fact, it is a cousin to the tetrahedron, the first of the Platonic solids.
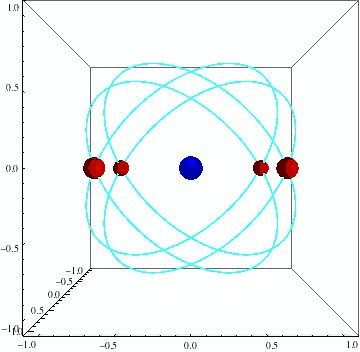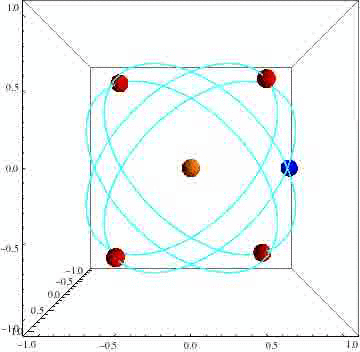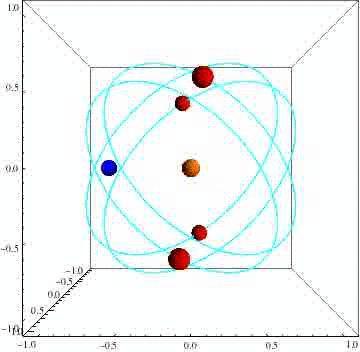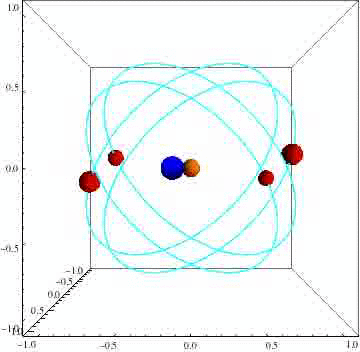
LISA’s three satellites might appear to be orbiting each other, but this is the result of an optical illusion. They’re really all orbiting the sun, “with their orbits cleverly arranged so that they approximately form an equilateral triangle at all times,” Boyle told Gizmodo. “The same is true of our very symmetric four-satellite orbit; the four satellites are really on four independent circular orbits around a central body.”
From then on, he was hooked. “I realised it was a super interesting object in its own right — more interesting than the original problem that had led me to it,” he said. “So I quit thinking about gravitational wave detection, and instead began thinking about whether I could find any other satellite orbits that were symmetric in this interesting new way.”
Boyle happened to mention his discovery of a dynamical analogue to the tetrahedron to a visiting cosmologist named Kendrick Smith (now a faculty member at Perimeter), wondering aloud if perhaps there were other such orbits corresponding to the rest of the Platonic solids. Smith came up with an ingenious mathematical solution to identify all possible symmetric orbits, regardless of the number of satellites. They dubbed them symmetric satellite swarms.
It all boils down to a more general phenomenon that Boyle calls choreographic order. And it’s applicable not just to space-based satellite systems, but also to modelling the microscopic structure of crystalline materials in Earth-bound laboratories — a class of so-called choreographic crystals.
“Instead of considering dances performed by satellites in circular orbit around the sun, we could instead think of analogous dances performed by electrons or nuclei movie through 2D or 3D space along straight-line trajectories,” Boyle said. “And the same mathematical techniques that let us systematically find all the choreographed satellite orbits could also be used to find all these more general choreographed dances.” As Phillip Ball writes at Physics Focus:
[I]magine two skaters moving simultaneously north-south and east-west through the center of a square rink and repeatedly reversing course when they reach the edges. The skaters have a higher choreography if they move out of phase — one reaching the edge while the other passes through the center — than if they are in phase, passing through the center at the same instant. In the first case, the moves capture the full symmetry of a square because the same set of rotations and reflections, along with time shifts, will leave the system unchanged. The second case has fewer symmetries. In general, says Boyle, there is a very large number of choreographic crystals, but only a few have very high choreography.
Thus far, choreographic crystals remain primarily mathematical objects, but Boyle and Smith think such structures could be found in nature. Their paper even proposes a simple diffraction experiment to find them, since it would reveal not just how the atoms are arranged in space within a crystal, but how those atoms move over time. Or perhaps they could be produced artificially.
And to think it all started with trying to design a better gravitational wave detector. “It’s like we followed a trail of sparkly things on the ground until, a year later, we looked up and found we had arrived somewhere very interesting, but very far from where we began,” said Boyle.
Reference:
Boyle, L., Khoo, J.Y., and Smith, K. (2016) “Symmetric satellite swarms and choreographic crystals,” Physical Review Letters 116: 015503.
Images: Boyle et al./Perimeter Institute