Many extreme roller coaster these days have vertical loops. Have you noticed that these loops are never circular? Why is this?
They all, also, seem to have the same similar ‘inverted teardrop’ appearance. Why is this?
Clearly there is the same physics and mathematics involved in their designs. Let’s take a look and see if we can derive a formula to describe their shape.
Back to School
First of all let’s go back to basics and understand how a loop works. Why doesn’t a coaster fall off the track when it goes inverted?

The answer is that there is a force (provided by the rails), that is pushing the trucks of the coaster towards the center of the loop.
This force is called the Centripetal Force.
Newton’s first Law of Motion of motion tells us that, without this force, the coaster would like to travel in a straight line and at constant speed. The centripetal force is pushing the coaster around in a circle. It is your body’s (equal and opposite) reaction to this force, often referred to as the Centrifugal Force, that explains the feeling you get of being squashed into your seat (Newton’s third Law of Motion).
Completing the trifecta, using Newton’s second Law, we know that with this Force is an acceleration (we’ll more strictly a rate of change of momentum but, hopefully, the mass of our coaster is constant!) When accelerating around in a circular path, the magnitude of the acceleration is proportional to the ratio of the speed squared over the radius of the curve.
The tighter the radius, or the higher the speed, the greater the acceleration.
How slow can you go?
The slowest speed that an (unattached) coaster can go around a loop upside down is at the limit at which the centripetal force is providedentirely by gravity. A rider in such a coaster would feel ‘weightless’ at the top of the loop (there being no reaction force provided by the track). Any slower, and the truck would fall off the rails!*

*In reality, coasters ride on tubular rails and are clamped by wheels on both sides (and passengers are safely harnessed into the carriages). Even if the coaster stopped completely, whilst you might be very uncomfortable, you’d still be safe.
Conservation of Energy
Roller coasters are typically not powered vehicles; at the start of the ride they are charged with gravitational potential energy then transfer this backwards and forwards to kinetic energy as they ride up and down the track.
If the loop were a perfectly circular arc then the trucks of the coaster would need to start at the bottom of the loop with sufficient enough kinetic energy such, after converting much of this to potential energy to climb, still has sufficient energy to just make it over the top.
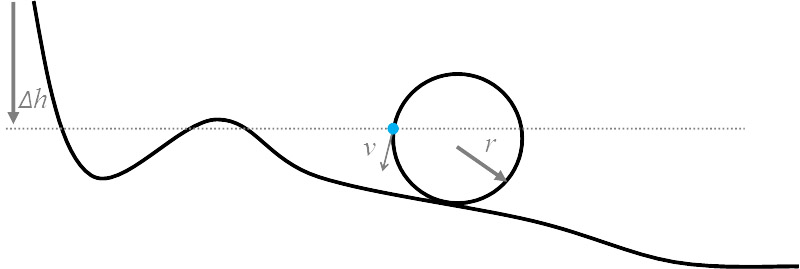
If the coaster starts are rest at the top of the ride, the velocity of the coaster at any point can be determined using the principle ofConservation of Energy. (We’re neglecting any effects of friction and wind resistance at this point).
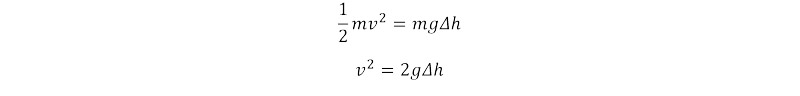
The centripetal acceleration experienced at any point on the ride can be expressed using the formula below in terms of the height from the release point of the coaster, gravity, and the local radius of curvature of the track:

“It’s not at the bottom, it’s not at the top…”
“…but this is the place that I always stop.” Robin the Frog (Halfway up the stairs, The Muppet Show)
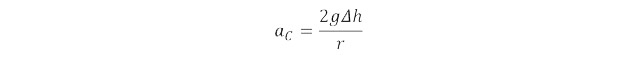
At the limit, at the top of the curve, when the centripetal acceleration is provided entirely by gravity g, we can see that this occurs when Δh = r/2
At the top of the loop (we’ll call this the 12 o’clock position), riders of the train will feel weightless. As the train continues around the loop to the 9 o’clock position, it will have dropped an additional Δh of r, resulting in a centripetal force of an additional +2g from that at the top.
At the bottom of the curve, there is an additional Δh of 2r, and this results in an additional acceleration at the bottom of +4g from that at the top, for a total centripetal acceleration of 5g. When this is added to the force experienced already experienced by the body, by gravity, this results in stress on the body of 6g. This is not good.
Even trained fighter pilots would eventually black out at sustained 6g loads (without the assistance of g-suits). This is supposed to be an amusement ride, not a James Bond like torture machine!
Clearly we need to rethink our roller coaster strategy. A circular loop has two very fundamental problems:
- The g-forces that a body is exposed to at the bottom of the loop exceed what is safe (when travelling at a speed that just allows the car to sail over the top of the loop).
- There will be a very rapid onset of this acceleration as the train starts the loop: The train would be playfully falling down the track, then wham! it will hit a 6g acceleration as it hits the bottom of the loop and starts its way up!
We need to come up with a better plan to address these two issues. We need to reduce the maximum g-force we expose our riders to, and also to come of with a more smooth mechanism for how to wind up and down these forces.
The root cause of the problem is that, as the coaster climbs, it looses speed as it trades its energy. We need to use this to our advantage. Maybe you can see the beginning of how we can address this by altering the radius of curvature of the track as our height increases and we lose energy?
Hold on, what if we are allowed to hang upside down?
As noted above, coasters are on rails, how about if we slowed the train down further so that it was (just about) at rest at the top?
The passengers would experience -1g as they hung from their straps at the top of the loop. This would result in a 5g load at the bottom (still unacceptable), and we’ve also not solved the jerky onset of this g load at the bottom.
Not a solution!
The speed needed at the entry of the loop (to allow the roaster to be able to crest over the top), creates too high an acceleration at the bottom!
The Solution
The solution to the first of the two problems (too high a g-load) is to decide on the maximum acceleration you wish to expose your riders to, then modify the track profile to keep this acceleration constant. As the coaster gains height, it loses speed. With this lower speed, the curvature of the track can be decreased to keep the needed centrifugal acceleration.

We know that the centripetal acceleration is proportional to v2/r, as the velocity reduces then we can decrease the radius to keep the acceleration a constant.
Before continuing with the coasters, let’s take a short detour and investigate this strategy further by looking at a simpler similar problem. One all in the horizontal plane where we don’t need to worry about gravity in the vertical plane.
Railroad Tracks and Roads
Imagine we have a straight railroad track. A train chugging along this track at constant speed is not experiencing any lateral forces or accelerations.
What happens when this train runs into a corner?
As soon as the curve is reached the train is subject to a lateral acceleration of v2/r. This appears with no warning or run up.
This might be fine at low speeds, but as the speed increases, the forces can be considerable. Nevermind the danger of derailment, or damage to the train, it also brutally uncomfortable for the passengers.
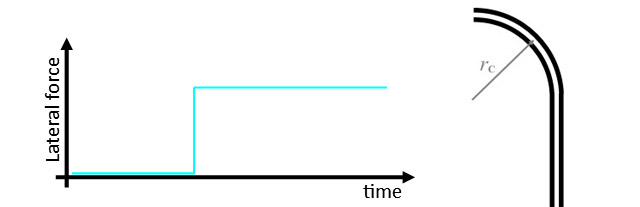
If you ran a model train track at excess speeds you probably found that it was at the entry to curves that the train derailed. A similar issue occurs if you enter a corner too fast with your model car race set.
Easing Into the Curve
What we want to do is gradually change the radius of the curve to slowly build up the acceleration (and thus ramp up the force gradually). There are an infinite number of ways for how we might select the profile for how the force is increased, but an obvious suggestion is a linear change.

Selecting a profile in which the force changes linearly with time (under the assumption that the velocity of the train does not change), can be achieved with a curve whose radius also changes linearly with time. This smooth transition is sometimes called an easement.
A curve whose radius changes linearly with angle (time) is a special kind of spiral called a Clothoid (also known as a Cornu spiral and even sometimes as a Euler spiral). Above you can see a Clothoid easement connecting the straight track to the circular track.
The easement starts parallel to the straight track, then curves gently. The curvature increases linearly until it meets at the circular track with the same radius of curvature as the circular track.
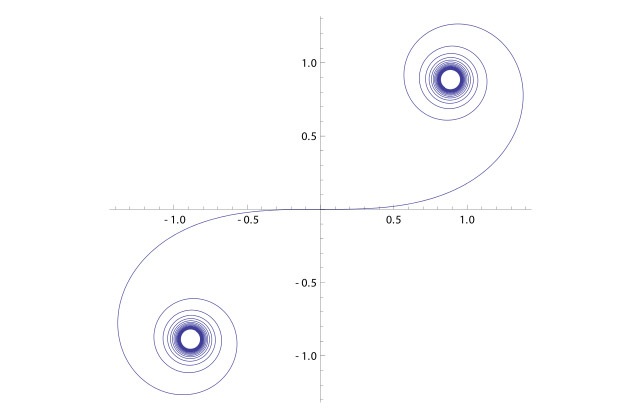
Here you can see a more complete rendering of a Clothoid. The curvature changes linearly with curve length.
Roads
Highway engineers love Clothoids as much as railway engineers.
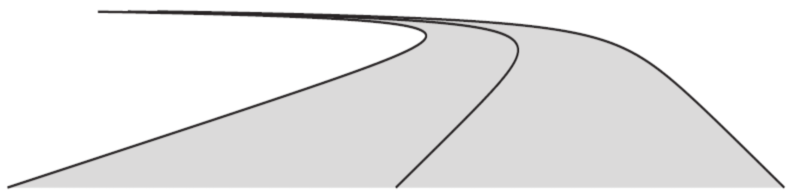
A road that employs a Clothoid easement curve, rather than a simple circular curve, reduces the stress and lateral forces on the tires of vehicles using it. When negotiating a Clothoid easement curve, at constant speed, a driver only needs to smoothly rotate his wheel with constant angular velocity.

According to research performed in Denmark, in addition, the perspective view of a road with a Clothoid curve is more natural and pleasing to the eyes (and allows more of the road to be seen). So, not only is the road easier to drive and steer on, and is less stressful and jarring to all occupants, it might even be safer by allowing the brain to better predict and see what is going to happen. I love mathematics!

Back to the Roller Coaster
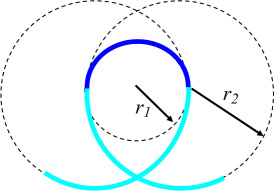
A first order approximate solution to the ideal roller coaster loop shape can be created by simply bolting together circular tracks of the appropriate radii.
A tight radius at the top where the speed is low, and a large radius at the bottom where the speed is high.
This is certainly a great improvement over an entirely circular arc, but still has the jerk accelerations at the bottom and at each of the transitions where the radius of the track changes.
Using what we learned from from our Clothoid investigation we can modify the radius of curve smoothly to keep a constant centripetal acceleration all around the loop. The shape of such a track is show to the right.

Constant G-Force
A Clothoid curve provides a ride that exposes the coaster to a constant centripetal acceleration, but the rider does not experience a constant g-ride because of gravity (and the changing relative direction this force acts).
The radius of the track at any point on the loop can be defined by the following equation:
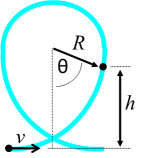
There is a resolved component of gravity acting on the coaster depending on it’s position around the curve. The Radius at any point can be determined using the following equation.
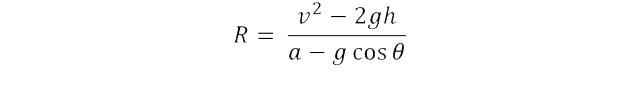
Where v is the speed going into the loop, h is the height from the bottom of the loop, a is the constant acceleration you want the riders to be exposed to, g is the gravity, and θ is the angle position around the loop that the truck is.
Putting It All Together
Using the above equation we can calculate the shape of the curve. Here it is plotted out:
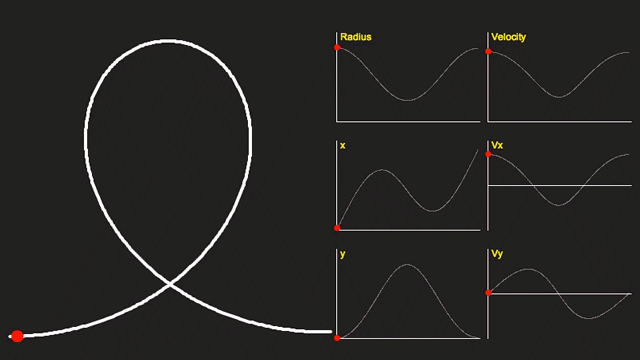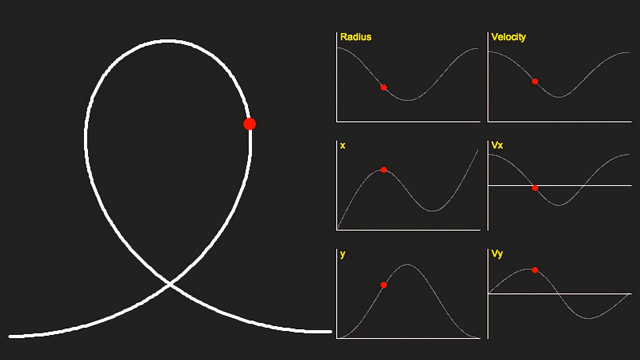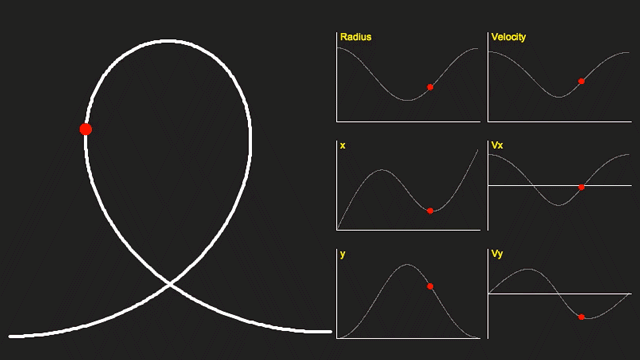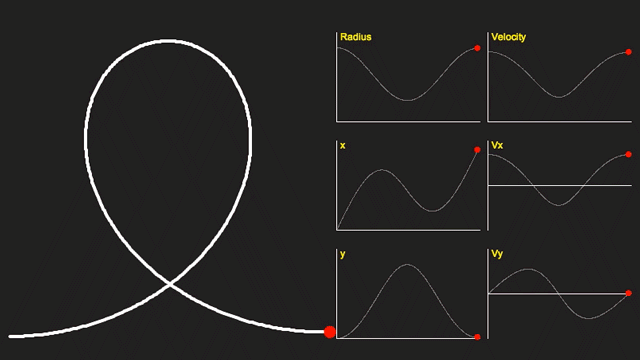
To the right of the curve are graphs showing the Radius of the curve, the x and y coordinates (x is positive to the right, and y is positive upwards), the absolute velocity, and the x and y components of this velocity.
You can see that the velocity and radius are at a minimum at the top of the loop (where the vertical velocity is also zero).
In Reality
In reality, we can’t ignore friction and air resistance, so these must be taken into consideration as well as a healthy safety measure. In addition, a real coaster is not a point mass, so there is rotational inertia to consider.
The coaster is also many cars long, so not all parts of the car are riding on the same radius. For instance, after cresting over the top and on the way down, the cars will be accelerating and picking up speeds. At this point, the last car still has not been passed the point of tightest radius. When it does pass, it will be travelling quicker and thus experience a higher acceleration.
Roller coaster enthusiasts exploit these differences and compare notes as to the better places to sit on each ride to maximise the hang times, g-forces and ride experiences.
Aerobatics
An opposite kind of problem occurs for aerobatic pilots.
A perfectly executed vertical loop starts at a fixed point, traces a perfect circle and returns to the same position, heading and altitude.

Unlike roller coasters, planes are powered and add energy to the system, but they still trade energy between kinetic and potential. As their speed decreases, so does the aerodynamic lift generated from their wing surfaces (Lift is proportional to speed squared).
As the speed bleeds off, rather than tightening the radius of the loop, the aim is to keep the radius constant.
An aerobatic pilot will, from horizontal level flight, pull the stick back hard (and suddenly) to initiate the loop (depending on the radius, exerting many g’s of load). He will use skill (and practice) to relax the stick to keep the arc circular as the speed bleeds off, all the way to the top. He will, then, reverse this strategy on the way down, ending the loop at the bottom pulling hard again.
If you want to read more about maths and general geekery, check out some of my other blog articles.
Image: Shutterstock/Marcio Jose Bastos Silva
This post was originally published on Data Genetics, a site created by Nick Berry was educated as a rocket scientist and aircraft designer, graduating with a Masters Degree in Aeronautical and Astronautical Engineering, and currenty works as a Data Scientist at Facebook. You can follow DataGenetics on Twitter here or on Facebook page here.
This post has been republished with permission from Nick Berry.
